SEMANA 14 MATEMÁTICAS

ABRIL 25 AL 29

CÓMO SACAR RAÍCES DE UN NÚMERO NATURAL, DESCOMPONIENDO EN FACTORES PRIMOS.

VER LOS TALLERES 4 Y 5 EN ESTE ENLACE




El siguiente algoritmo se basa en aplicar los siguientes teoremas:
"La radicación de un producto es igual a la radicación de los factores por separado."
"La radicación de una potencia es igual a la base de la potencia elevado a la división del exponente con el índice de la radicación."

Aquí el algoritmo:

• Se descompone el radicando en sus factores primos.
• Se expresa el radicando en una multiplicación de potencias.
• Se separan los potencias en radicaciones por separado.
• Se operan las raíces por separado.
• Se multiplican los factores que quedan.

Ejemplo.

Hallar la raíz cuadrada por descomposición en factores primos de 900
Se descompone 900 en factores primos




1. Se expresa 900 en una multiplicación de potencias




2. Se separan las potencias en radicaciones por separado.




3. Se operan las raíces por separado.




4. Se multiplican los factores que quedan y obtenemos

Criterio de divisibilidad por 7

Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7.
Ejemplo:


343 34 − 2 · 3 = 28 28 es múltiplo de 7

105 10 − 5 · 2 = 0

2 261 226 − 1 · 2 = 224
Se repite el proceso con 224 22 − 4 · 2 = 14 14 es múltiplo de 7

Criterio de divisibilidad por 11

Un número es divisible por 11, si la diferencia entre la suma de las cifras que ocupan los lugares impares y la de los pares es 0 o un múltiplo de 11.
Ejemplo:


121 (1 + 1) − 2 = 0

4224 (4 + 2) − (2 + 4) = 0


Otros criterios de divisibilidad

Criterio de divisibilidad por 4

Un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.
Ejemplo:
36, 400, 1 028, ...

Criterio de divisibilidad por 8

Un número es divisible por 8, si sus tres últimas cifras son ceros o múltiplo de 8.
Ejemplo:
4 000, 1 048, 1 512, ...
Criterio de divisibilidad por 9

Un número es divisible por 9, si la suma de sus dígitos es múltiplo de 9.
Ejemplo:


81 8 + 1 = 9

3 663 3 + 6 + 6 + 3 = 18 18 es múltiplo de 9

NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS.

Nota: esto es sólo para números enteros mayores que 1
Es decir: 2,3,4,5,6,7,8,9,10,11,12,... etc

Un número primo se puede dividir exactamente sólo entre 1 y él mismo.

Un número compuesto se puede dividir exactamente entre otros números además de 1 y él mismo.

(Así que cualquier número entero mayor que 1 es primo o compuesto)

Ejemplos

Número	Se puede dividir exactamente entre	¿Primo o compuesto?
1	(1 no es primo ni compuesto)
2	1,2	Primo
3	1,3	Primo
4	1,2,4	Compuesto
5	1,5	Primo
6	1,2,3,6	Compuesto
7	1,7	Primo
8	1,2,4,8	Compuesto
9	1,3,9	Compuesto
10	1,2,5,10	Compuesto

Factores

Los "factores" son los números que multiplicas para llegar a otro número:

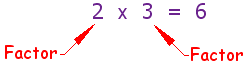
Algunos números se pueden factorizar de muchas maneras:

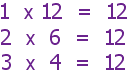
TALLER DE APLICACIÓN SEMANA 14

1.Aplicar criterios de divisibilidad por 4, 7, 8, 9 y 11 a números naturales dados.

2.Clasificar números en primos y compuestos.

3.Sacar raíces cuadradas y cúbicas de números naturales dados, por descomposición en factores primos.