REPASO POLINOMIOS ARITMÉTICOS CON NATURALES.
APLICACIÓN DE LA PRUEBA DEL CONOCIMIENTO DE FINAL DE PERÍODO.
Una diagonal de un polígono es un segmento que une dos vértices no consecutivos

Cuántas diagonales se pueden trazar desde un olo vértice?
Aplico la fórmula n-3; donde n es el número de lados del polígono dado.
ver el video
Cómo encontrar el número de diagonales totales de un polígono?
Se aplica la fórmula: ver el video .
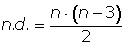



Ángulos interiores de polígonos
Un ángulo interior es un ángulo dentro de una figura.
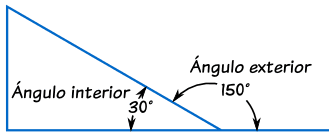
Triángulos
Los ángulos interiores de un triángulo suman 180°
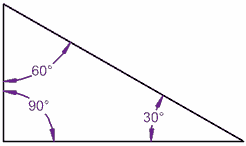 | 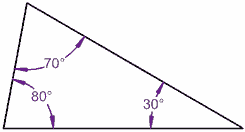 |
90° + 60° + 30° = 180° | 80° + 70° + 30° = 180° |
¡En este triángulo es verdad!
|
Vamos a inclinar una línea 10° ...
También funciona, porque un ángulo aumentó 10°, pero otro disminuyó 10°
|
Cuadriláteros (cuadrados, etc.)
(Un cuadrilátero es una figura de 4 lados)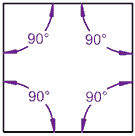 | 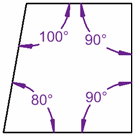 |
90° + 90° + 90° + 90° = 360° | 80° + 100° + 90° + 90° = 360° |
Un cuadrado suma 360°
|
Vamos a inclinar una línea 10° ... ¡también suman 360°!
|
Los ángulos interiores de un cuadrilátero suman 360° | |
Porque en un cuadrado hay dos triángulos
| Los ángulos interiores de este triángulo suman 180° (90°+45°+45°=180°) | 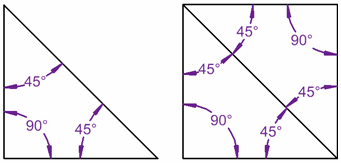 |
... y los de este cuadrado360°
... ¡porque el cuadrado está hecho de dos triángulos!
|
Pentágono
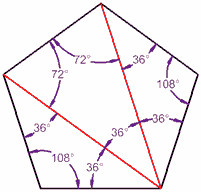 |
Un pentágono tiene 5 lados, y se puede dividir en tres triángulos, así que ...
... sus ángulos interiores suman 3 × 180° = 540°
Y si es regular (todos los ángulos son iguales), cada uno mide 540° / 5 = 108°
(Ejercicio: asegúrate de que cada triángulo aquí suma 180°, y comprueba que los ángulos interiores del pentágono suman 540°)
|
La regla general
Así que cada vez que añadimos un lado más (de triángulo a cuadrilátero, a pentágono, etc) sumamos otros 180° al total:
| Si es regular... | ||||
| Figura | Lados | Suma de los ángulos interiores | Forma | Cada ángulo |
|---|---|---|---|---|
| Triángulo | 3 | 180° | 60° | |
| Quadrilátero | 4 | 360° | 90° | |
| Pentágono | 5 | 540° | 108° | |
| Hexágono | 6 | 720° | 120° | |
| ... | ... | .. | ... | ... |
| Cualquier polígono | n | (n-2) × 180° | (n-2) × 180° / n | |
La última línea puede ser un poco difícil de entender, así que vamos a ver un ejemplo.
Ejemplo: ¿Qué pasa con un decágono (10 lados)?
 |
Suma de los ángulos interiores = (n-2) × 180° = (10-2)×180° = 8×180° = 1440°
Y, si es regular, cada ángulo interior = 1440°/10 = 144° |
No hay comentarios:
Publicar un comentario